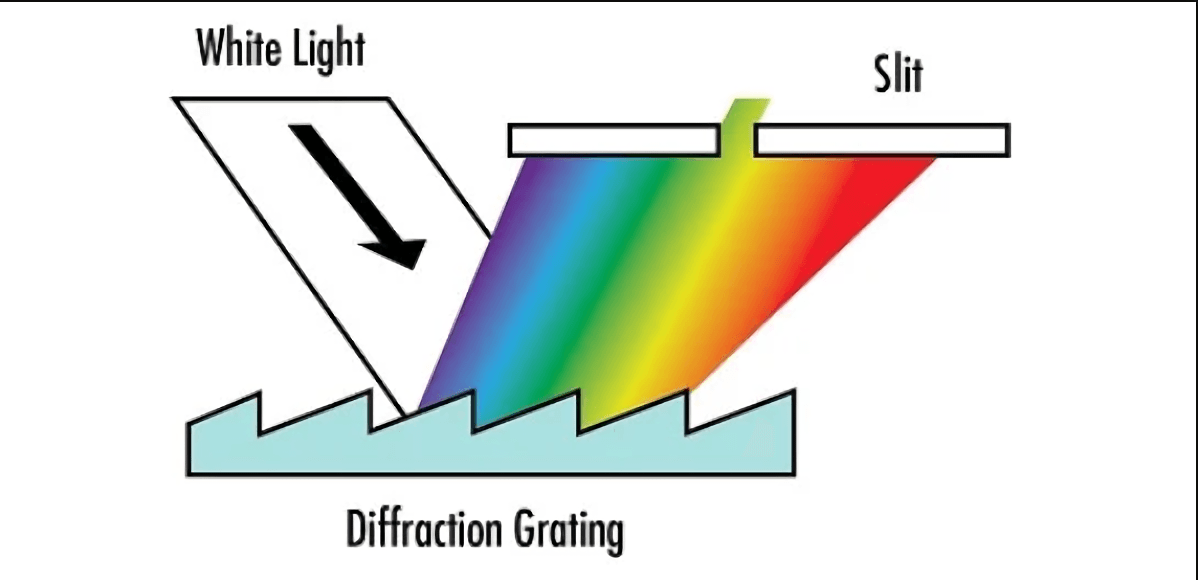
最简单的衍射光栅是在不透明材料上具有一排周期性分布的裂缝,如图2.3.10a所示。入射光波在一定的方向上被衍射,该方向与波长和光栅特性有关。图2.3.10b表示光通过有限数量的裂缝后,接收到的衍射光强分布。由图可见,沿一定的方向(θ)具有很强的衍射光束,根据它们出现位置的不同,分别标记为零阶(中心)及其分布在其两侧的一阶和二阶光波等。假如光通过无限数量的裂缝,则衍射光波具有相同的强度。事实上,任何折射率的周期性变化,都可以作为衍射光栅,衍射光栅解复用器将在后面介绍。

我们假定入射光束是平行波,因此裂缝变成相干光源。并假定每个裂缝的宽度a比把裂缝分开的距离d更小,如图2.3.10a所示。从两个相邻裂缝以角度θ发射的光波间的路径差是dsinθ,由式(2.2.3)可知,Δz=dsinθ=(Δϕ/2π)λ=mλ,令m=Δϕ/2π,所以,所有这些从一对相邻裂缝发射的光波相长干涉的条件是路径差dsinθ一定是波长的整数倍,即

很显然,相消干涉的条件是路径差dsinθ一定要等于半波长的整数倍,即
式(2.3.3)就是著名的衍射方程,有时也称为布拉格衍射条件,式中m值决定衍射的阶数,m=0对应零阶衍射,m=±1对应一阶衍射,……当a<d时,衍射光束的幅度被单个裂缝的衍射幅度调制,如图2.3.10b所示。由式(2.3.3)可见,不同波长的光对应不同长度的距离d,因此,衍射光栅可以把不同波长的入射光分开,它已被广泛应用到光谱分析仪中。
威廉·亨利·布拉格(图2.3.10c)与其子威廉·劳伦斯·布拉格皆为英国著名物理学家,通过对X射线谱的研究,提出晶体衍射理论,建立了布拉格公式(布拉格定律),并改进了X射线分光计。
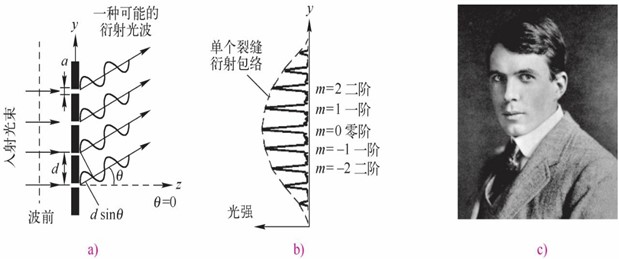
图2.3.10衍射光栅
a)有限裂缝数衍射光栅 b)接收到的衍射光强分布
c)威廉·亨利·布拉格(W.L.Bragg)
c)威廉·亨利·布拉格(W.L.Bragg)